謎の数列「1→1→2→3→５→8→13…」の正体は？？黄金比にも使われるあの数列【数学/21年12月21日さくっと解説】

こぼねろらいふ
2021.12.21

きょうの問題はコレだ！

スポンサーリンク

さくっと解説

二つ前の数字を考える

今回の数列は、1つ前の数字と2つ前の数字に注目すると今回の答えが見えてきます。

”3”について注目すると、1つ前は"2"で2つ前は”1"です。
この1と2が3にどう関係しているかというと…

もうわかりましたね！

足し算です！
1+2＝3

今回の数列はすべてこの法則で成り立っています。
そこから答えが見えてくるでしょう！

〇の前は、2と3なので足し算をして
〇＝5

△の前は、8と13なのでそれも足し算して
△＝21

したがって、〇＝5,△＝21

フィボナッチ数列

今回の数列は、有名な数列の一つである、
「フィボナッチ数列」です。

イタリアの数学者であるレオナルド・フィボナッチさんによって名付けられた数列です。

どの数も2つ前の数を足したものになるという数列。

なぜここまで有名なのかというと、いくつか理由があるのですが、
一つに、自然界にたくさん使われているというのがあります。

自然界

植物の花びらの数がフィボナッチ数列になっていたり、有名なもので行くとひまわりの花の螺旋がフィボナッチ数列になっています。
もう一つ植物関連で行くと、茎への葉っぱのつき方がこの数列になっていたりします。

黄金比

植物以外でいくと、黄金比があります。
フィボナッチ数列によって構成された螺旋は世界で最も美しい螺旋と言われていたり、さらにその数列によって作られた螺旋は、1:1.618という黄金比の近似値でもあります。

まぁこんな図ですよ！

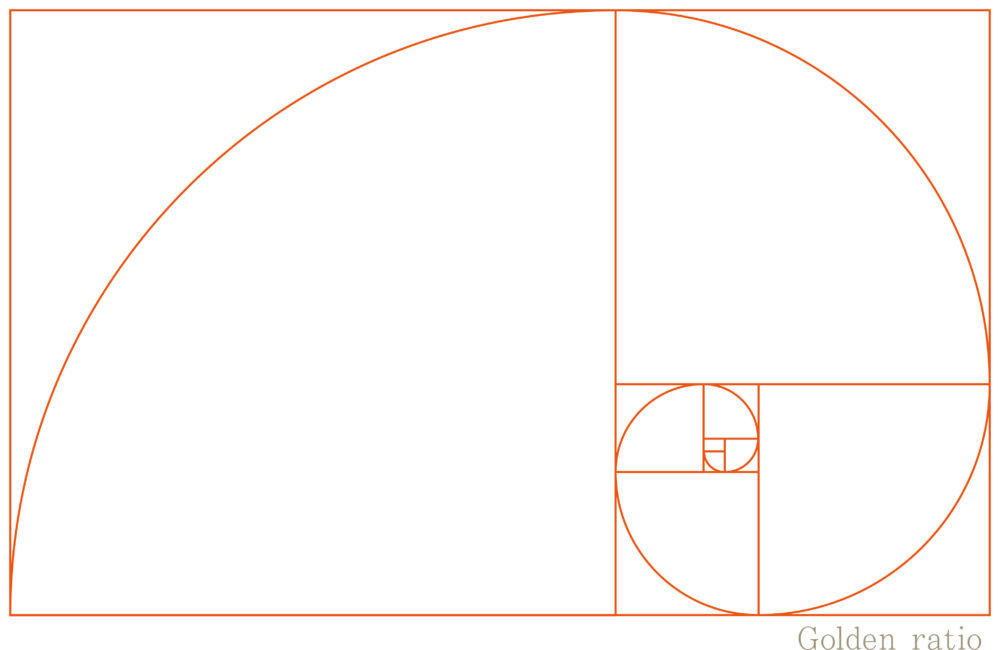
フィボナッチ数列はこのように、結構日常の中で使われています！
雑談のネタに使ってみるのもいいかもしれませんね！！

こぼねろのおすすめ

数学は、今回のフィボナッチ数列のように日常にたくさん生かされています。
そんな数学の面白い知識を集めた本がこちらです！！

お話のネタにも、寝る前に読む本としてもおすすめですよ✨

笑う数学　著：日本お笑い数学協会
くだらなすぎて笑える話から、ガチで試験に使える話まで詰まった数学本

パート2を√4と表記しているところもおもいろいですね笑

次回のヒント

インフレの真逆の減少のこと！

まぁこの時点で、「1.インフレ」は答えじゃないね！

スポンサーリンク

コメント